Polycubes
Introduction
Polycubes. Like polyomines but pure chunky like.
There's one monocube. That's the cube. And there's one dicube, I guess it would be called, a 2x1x1 rectangle that you can't do a lot with. There are two tricubes, and these are just the 'chunky' versions of the two triominoes. You can't really do too much with these either.
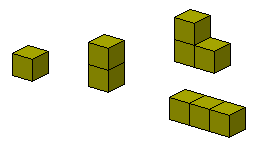
Fig. 1: the monocube (a.k.a. the cube), dicube and two tricubes
Sure, there's the 3D versions of the little trivial things you can make with the triominoes: the stairstep shape from the two tricubes, or the 3x3x1 from the 1, 2 and 3-cubes all together. But these aren't exactly challenging or interesting, let's face it.
Fig. 2: Truly riveting stuff.
I never thought the tetracubes would be particularly interesting. I assumed that if they could make any cuboids or other shapes, I'd be able to buy a set from somewhere. And I assumed that the existence of the Soma Cube was because the mathematically-complete set of tetracubes wasn't much fun and this was the next best thing.
I thought wrong.
Tetracubes
There are 8 tetracubes, if you count the top-left and top-right in the image below as two distinct shapes since you can't rotate one and get the other. Five are just the tetrominoes with an extra sprinkling of depth (the planar tetracubes) and the other three are brand spanking new. Together these have a total of 8x4=32 unit cubes. And since these aren't limited by parity issues the way tetrominoes are, there are a few nice rectangles you can knock together with these.

Fig. 3: The tetracubes (or a crude approximation thereof)
Making a set of these yourself is strongly encouraged. I did. Or I attempted to anyway. I grabbed a bunch of wooden cubes off eBay and glued them up one morning, only to realise afterwards that the cubes weren't as cubic as I'd have liked, so the shapes were a tad uneven. Still, they do the job.
The first thing I was delighted to find out was that these eight pieces can form a 2x2x4 cuboid. There are 1,390 ways of doing this but it's bloody hard. Or at least I had a right job with it. Then, just after I'd calmed down from the sheer excitement of finding out a 2x2x4 was possible, I found out that a 2x2x8 was possible too!
In fact, the pieces can be made into two little 2x2x4 cuboids as in the image below, then these two cuboids can be arranged into either a 2x2x8 or the 2x4x4:

Fig. 4: Cuboid solutions, colour-coded because I have no idea how else to represent 3D solutions as images.
Exciting stuff! Actually, this is about as far as I got playing with these. Obviously, 1xnxn rectangles are ruled out because three of the pieces stick out 2 squares in every direction. And I haven't found many other nice constructions (so far) while just playing around. (But that doesn't mean they're not out there, just that I'm far too lazy.)
Really, deep down, part of me just wants to buy some more wooden cubes and make a set of wonky-but-usable pentacubes. There are 29 of these bad lads (12 planar pentacubes and 17 that really utilise that third dimension), which is a bit of a shame because that gives 29x5 = 145 unit cubes which can't be split up into 3 factors, which means that solid cuboids are out. But some computer searching revealed that a 7x7x3 cuboid with a 2-cell deep central 'well' is totally possible. So if I was to make a set, I'd maybe include the 2x2x1 dicube and sacrifice a little bit of mathematical completeness for prettiness. And if my woodworking skills weren't utterly atrocious I'd consider making a nice little box that holds all 30 pieces in the 3x7x7 shape. And give it a hinged lid or something too while we're at it.
Having said that, I hate puzzles that have to be solved in order to be put away properly. I have this set of wooden pentominoes (and one tetromino) that fit into an 8x8 box but to put the lid on and have it all nice and tidy, you've got to solve the thing first, and it drives me up the wall.
Making scaled-up Tetracubes
The total volume of the tetracubes is 32 units, which is just enough to construct a big tetracube scaled up by a factor of two. For four of the five planar tetracubes and two of the non-planar ones this is trivial once we've got the two 2x2x4 blocks above solved, just put them together in whichever configuration. For the two remaining tetracubes - the T-tetromino and the cyan one bottom left in the image above - it's a little more tricky.
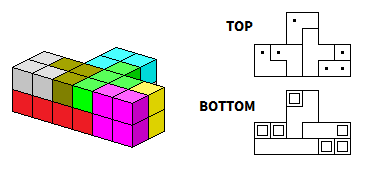
For the diagram on the right, a dot indicates that that piece extends into the layer below there, and a
square indicates that it extends into the layer above. This appears to be the exact opposite of the
convention used over at the Poly Pages, which is an oversight on my part. Oops.
The solution for the T-tetromino is shown above, but the final tetracube is a challenge for the reader. It's possible, but I can't be bothered to draw out another diagram for it so you'll have to find it yourself.
Almost-cuboids
There are also the two cuboids-with-holes-in-them that can be done. There's the 2x3x6 with a 1x1x4 hole, and the 3x3x4 with a 1x2x2 hole. I imagine there are several ways to solve each, but I've included once possibility for each, in the same probably-wrong notation as above.
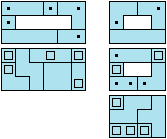
Next: Octomino Prisms with the Tetracubes
[ Home > Polycubes > Introduction ]
Lewis Patterson. Last updated 14/10/2021.