Combining Pentominoes and Hexominoes
(into one nice big happy family)
Introduction
Hexominoes kinda suck. Well, they don't but they have all sorts of issues like parity imbalance and such which prevents them from being as versatile as they probably ought to be. There are a few ways to address these issues, including considering the one-sided hexominoes, but another (albeit less mathematically 'pure' set of pieces to consider is the set of pentominoes and hexominoes togather.
Rectangles
Thirty-five hexominoes at 6 square units each + Twelve pentominoes at 5 units gives a grand total of 270 units² to work with. And 270 factorises in lots of ways. Obviously, 1x270 and 2x135 are out right away, and as for 3x90 while I can't prove it directly I have a hunch there's too much perimeter for the pieces to be able to fully cover. Maybe it does have a solution, like the thin solution with the pentahexes, but I don't have the balls to go looking for it.
5x54 is where things start to get definitely possible, and the rest of the possible rectangles (6x45, 9x30, 10x27 and 15 by whatever 270 divided by 15 is) are all easy enough to solve by hand if you don't mind a little trial and error.

Fig. 1: Rectangles using the combined sets of pentominoes and hexominoes.
Solving these by hand is a touch easier than solving purely hexomino constructions by hand. The fact we've got some of the more friendly pentominoes to use alongside the nicer hexominoes at the end of a solution goes a long way. I would heartily recommend getting yourself a set of these. Buy them, make them, hack them out of the back of a cereal box, whatever it takes. You won't regret it.*
* Polyominoes.co.uk accepts no responsibility for any regret caused by the acquisition of any polyform sets.
Rectangles 2: The Revenge
Since 270 divides up so well, not only can you make rectangles but you can do sets of congruent smaller rectangles too! Check it out:
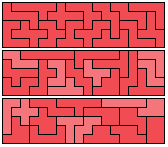
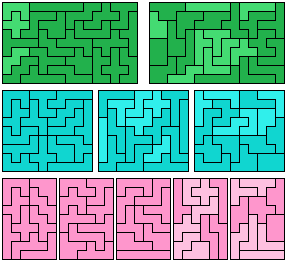
Fig. 2: Three 5x18s, two 9x15s, three 9x10s and five 6x9s.
The challenge here is making sure you have the right balance of pent- and hexominoes in each rectangle. For example, for the bottom row (the five pink 6x9s) each rectangle is 54 units, and the only way to get 54 by adding 5's and 6's is either nine hexominoes (9x6) or six pentominoes and four hexominoes (6x5 + 4x6 = 54).
For the same sort of reason, we can rule out six 5x9s. Each rectangle would have 45 units, which can only be filled by 3 pentominoes and 5 hexominoes (since 3x5 + 5x6 = 45) but that would require 15 pentominoes total so it can't be done :(
Nine 5x6s is out too. A 30-cell rectangle must have either 0 or 6 pentominoes so that the remainder can be filled with hexominoes - that is, it must be either all pent or all hex. This would mean that all the hexominoes would end up together in seven 5x6 blocks... but then you could just push those together and make a 6x21 rectangle of pure hexominoes, which ain't possible because of parity constraints.
Parallelograms
Moving on to some less rectangular shapes...
Again, we've got a lot of variety possible here - the base lengths 6, 9, 10, 15, 18, 27, 30, 45 and 54 are solvable in theory, but in reality it's a little bit of a different story.
Of these, I've only done a selection of these by hand, mainly because they're not massively challenging or interesting (then again, if I didn't bang on about uninteresting things here this website would be empty.) The longer the diagonal sides, the trickier it is, just because you run out of wiggly pieces building one side then have to use the nice easy pieces on the second side.
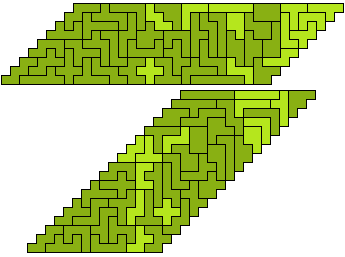
Fig. 3: Two example parallelograms. You can solve the rest yourself (with that newly-acquired set of pieces of yours!) because it takes so long to transfer them from notebook sketches into pretty diagrams and it's really not worth it for not-that-interesting solutions like these.
Of course, you don't need to stop there. With the aid of computer search ('cause I'm lazy like that) I found the following two even taller skinnier parallelograms
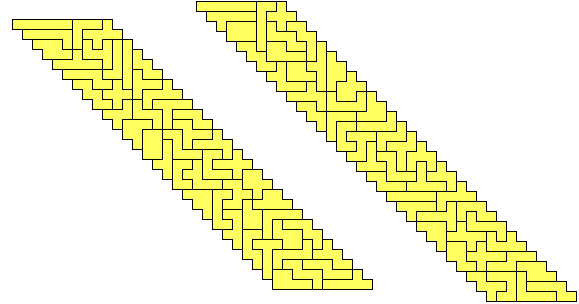
Fig. 4: Just look at these freaks of nature. And I'm willing to bet the even thinner 6x45 is possible too, but so far FlatPoly2 has failed me.
Rectangles with little bits missing from inside 'em
...because not only does 270 factorise well, but some of the numbers just above it factorise fairly nicely too!
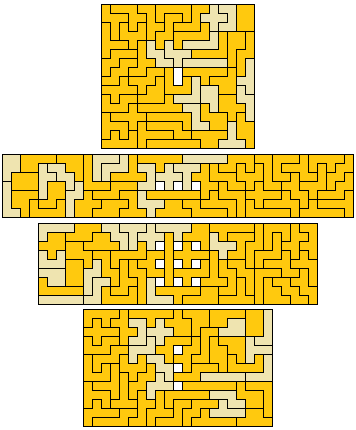
Fig. 5: Holey rectangles. (I fought the urge to follow that with 'Batman', I hope you appreciate that.)
Getting All Fancy
Depending on how much you like solving wiggly diagonal edges there are all sorts of other possibilities too, so long as you don't mind the odd hole slap-bang in the middle of everything. Check out the following bad lads, sorted in order of how many tears were shed before finding the solution:

Fig. 6: Various other shapes. The limit is your imagination!
That central heptomino is completely arbitrary really, it's just the most fitting one that has a few axes of symmetry. The same patterns could be done with a hole the shape of the H-looking heptomino (for example) but it just doesn't look as neat.
Another option (which to be honest I haven't really looked at myself on account of being proper lazy) is putting additional restrictions on the way the pentominoes are distributed, for example, making sure that each pentomino isn't touching any others, or that they are all bunched together in particular ways. The solution below has the pentominoes grouped into two symmetrical end bits. Actually, I didn't solve this one thinking about it as a pent+hex construction, I did the middle hexomino bit and only realised the two pentomino end caps were possible a while later.

Fig. 7: A nice five-cell high pattern with the pentominoes bunched together at each end all nice and symmetrical.
Other Possibilities
A slightly more complete-feeling set would be the entire range of 1 through 6-ominoes, but sadly, their total area is 299 units, which you can't really do a lot with. There's a 13x23 rectangle, and by extension two 13x23 parallelograms, and adding a unit cell hole allows things like the 24x24 right-angled triangle.
But then you've got monominoes and monomino-sized holes together in the same construction, which just isn't very aesthetically pleasing for some reason. And since you've got all the tiny little triomino, domino and monomino pieces to work with, these aren't that much of a challenge either. So it's not such a good set after all.
[ Home > Polyominoes > Combining Pentominoes and Hexominoes ]
Lewis Patterson. Last updated 21/04/2021.