Polyaboloes / Polytans
Polytans (also polyaboloes, depending on which website you're looking at) are the shapes made from joining isoceles right-angled triangles (45-45-90 triangles, or the triangle you get when you chop a square in half diagonally) together edge-to-edge. Theres one 1-tan, which is just the triangle on its own, then three 2-tans, four 3-tans (tritans? triaboloes?) and 14 tetratans/tetraboloes. The numbers grow colossally fast compared to the numbers of polyominoes, polyiamonds or just about anything else; probably because there's often more than way to append a triangle to an edge.
Here's some pretty pictures of the 1- through 4-tans, courtesy of a tedious as balls half-hour in Microsoft Paint. Upon completing this I realised I could have just generated them using Peter Esser's solver and took a screen shot. You live and learn.
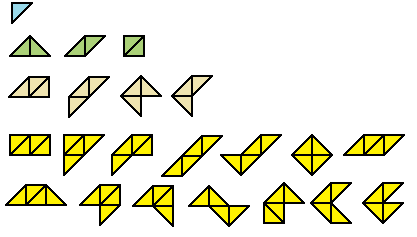
Beyond this, there are 30 penta-tans, 107 hexa-tans, 318 hepta-tans and none of those look like real words, I can kinda see why the -aboloes suffix gets used. Yeah, pentaboloes and hexaboloes rolls off the tongue a lot better. Here are counts for the free, one-sided and fixed n-aboloes up to n = 8:
| n | Free | One-sided | Fixed |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 3 | 4 | 9 |
| 3 | 4 | 6 | 24 |
| 4 | 14 | 22 | 71 |
| 5 | 30 | 56 | 224 |
| 6 | 107 | 198 | 740 |
| 7 | 318 | 624 | ? |
| 8 | 1116 | 2182 | ? |
The counts for fixed polyaboloes may not be correct because I couldn't find them anywhere on the internet to cross-reference with. So don't quote me on those.
I have made little acrylic sets of the 1- to 4-aboloes to play with. The larger sets I haven't gotten around to doing yet, mainly because I've only got so much annual budget for polyomino-related spending. But tetraboloes are more than enough of a fiendish challenge in the mean time.

Fig. 2: Courtesy of a really cheap mobile phone camera.
The combined area covered by the triaboloes and tetraboloes is 34 which is a bit of an ugly number but it's still workable. For a start, we can do rectangles of area 36 with the corners snipped off, as in the image below. this works for 6x6, 4x9 and 3x12 rectangles. (2x18 looks to be impossible.) Difficulty-wise, the thin rectangle doesn't seem noticeably easier or harder than the square, but then again they're all infuriatingly tricky for something so deceptively simple-looking. Best technique seems to be to try and use up pieces with lots of diagonal edges first. But that only gets you so far. Prepare for lots of trial and error.
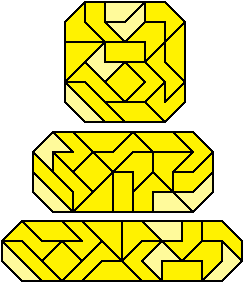
This set of pieces (the combined tri- and tetraboloes) was originally discovered by Wen-Shan Kao under the name 'ProTangram' long before I found it. There are several other challenges using this set of pieces listed over at this site, along with enumerations of solutions for each configuration.
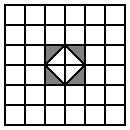
On the back of the tray I made for my set there's the following configuration, which is just unfairly difficult. The centre requires the square-shaped bit, leaving the remaining 17 pieces to fill the square doughnut around it. There are 30 solutions to this but finding even one of them manually is something of an ordeal (click here too see them if you don't want to have a crack at solving it yourself first.)
Pentaboloes
Pentaboloes are the next set in the sequence - the shapes made by attaching five of those triangles:

Notice how I was too lazy to trim the edges off the bottom of the tray. And too lazy to paint or varnish or do anything with the pieces.
There are 30 of these in total. Mine are made of MDF, lightly toasted by the laser that cut them. 30 multiplied by 2.5 gives a total area of 75 unit squares, which feels like it should be a good thing; it's not prime or anything. But it means that for rectangles (the most obvious shape to try and pack a set of pieces into) we've only got one option - 5x15 - and it just doesn't seem to be possible. I've tried by hand, and I've let Peter Esser's mops solver churn away at it in the background while writing this, and it seems to get a maximum of 29 pieces placed but no higher. I'm wondering if parity has a filthy triangular cousin, or maybe there's a lack of available orthogonal edge sections within the set of pieces to fully build a rectangle with 40 units of edge.
(This is the point where a proper polyform website would launch into an investigation of just why the 5x15 doesn't seem to be possible, but this is polyominoes.co.uk so don't kid yourselves, all you're getting from me is a shrug and a suggestion to look into it yourself.)
You get slightly better luck with a 7x11 rectangle with the corners snipped off. I have a solution saved from ages ago and I can't remember if it was found by hand or by computer. And there's no obvious way to tell either. With sets of pieces like the n-ominoes for n > 5, I generally save certain pieces for last, so there's a visible gradient across a human-found solution going from wiggly nasty pieces all the way to big blocky square pieces. But with these there are only like three or four really nice pieces - the three consisting of a domino with a half-square attached to it somewhere. And they all end up properly mixed in with the other pieces. Finishing a solution with these is much more perseverance than technique.
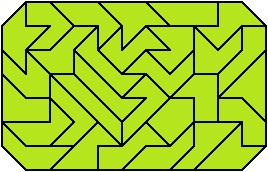
One other thing you can do with these that's fractionally easier than solving just using the pure pentaboloes set is to introduce the triaboloes (or tri-tans if you call them that) into the mix, and solve things with an area of 81 units². Here's one of many solutions to the 9x9; this was solved by hand, and it took an absolute age... I just left it unfinished on my desk then ever so often took a punt, desperately rearranging a few pieces. And then one day, after several cumulative hours of trying, the bits I happened to have left fell perfectly into place. This solution has the four triaboloes separated from each other, which looks nice but was entirely unintentional.

There'll be a solution where all four triaboloes are bunched together in one clump, but finding that can be a job for someone else.
I have been toying with the idea of getting the hexaboloes laser cut at some point, but I get the feeling they're going to be even more of an endurance test than these, which doesn't fill me with a lot of motivation.
[ Home > Polyaboloes ]
Lewis Patterson. Last updated 26/11/22.