Planar Heptacubes (The Lazy Way)
Usually polycube constructions are beyond my capability, since I don't own any physical sets beyond the tetracubes and have a computer that would probably struggle to find things with sets much larger than pentacubes. (I think hexacubes have a checkerboard parity issue just like the hexominoes as well, which makes the prospect all the more terrifying.) But recently I realised something about the set of thee 108 planar heptacubes that could make a few solutions possible despite only owning a set of bog-standard heptominoes.
Of the planar heptacubes the only one that really needs any special attention is the harbour heptomino equivalent. Unlike the case with regular heptominoes it doesn't force a hole in the construction, but it does sort of require that it must be placed perpendicular to whichever heptacube is filling its hole. At some point a few days ago I realised that if the harbour heptacube (it feels weird calling it that somehow) was 'neutralised' by a small number of pieces then I could solve the rest of the heptacube construction purely in layers using my existing set of heptominoes. Saving me from having to cut up and glue 108 pieces. Which I'll do eventually, just not now. The tetracubes were already pushing the limits of what I can make.
It turns out that two other heptacubes are enough to make a little bullet-heptomino-prism that can be slipped into the corner of a 3x14x18 cuboid, leaving three layers with a multiple of 7 cubes that can be solved manually. Something similar is probably possible for a 6-layer cuboid, 6x9x14 maybe.
Or a 4x9x21... And solving into four rectangles is a lot less painful than solving six... Anyway, here it is:
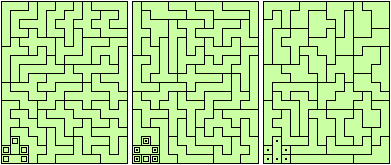
As usual, dots indicate that a piece extends down into the layer below, and a little square means it extends up into the later above. In this case the three heptacubes that lie perpendicular to the plane so to speak are the analogues of the pi and harbour heptomino and the one that looks like a little H inside a 3x3 box.
Here's a view of it as a nice isometric image, a needless victory lap purely because I learnt how to use Inkscape recently and want to show off:

If I ever manage to solve anything else with the larger polyiamond sets, at least I can now guarantee that the images will look a little better than the old ones do.
A few hours after finding this, the urge to solve the 4x9x21 became too difficult to resist, and after about an hour or so I had the following solution using the exact same trick as the 3x14x18 for dealing with the harbour piece:


If I ever decide to make a set of these, a little 4x9x21 storage box would probably work quite well.
There's undoubtedly a 6-layer cuboid out there, a 6x9x14 or something, but more rectangles = more problems so I haven't attempted looking for it yet. It'll be within the realms of a hybrid solve - me manually filling the first 4 or 5 layers then letting FlayPoly2 chew on the remaining bits. But there's not usually a great deal of satisfaction in solving things that way. So it can wait.
[ Home > Polycubes > Planar Heptacubes ]
Lewis Patterson. Last updated 04/02/23.