More things you can do with pentahexes
...if you're into that sort of thing
Parallelograms
110 divides up fairly nicely, so you've got possibilities for 5x22 and 10x11 parallelograms. Or approximations thereof, they're all going to have wiggly edges what with being made of hexagons and all. The 2x55 is impossible because some of the pentahexes are 3 hexagons tall in multiple directions.

You can also subdivide further and make two 5x11s with 11 pieces each.
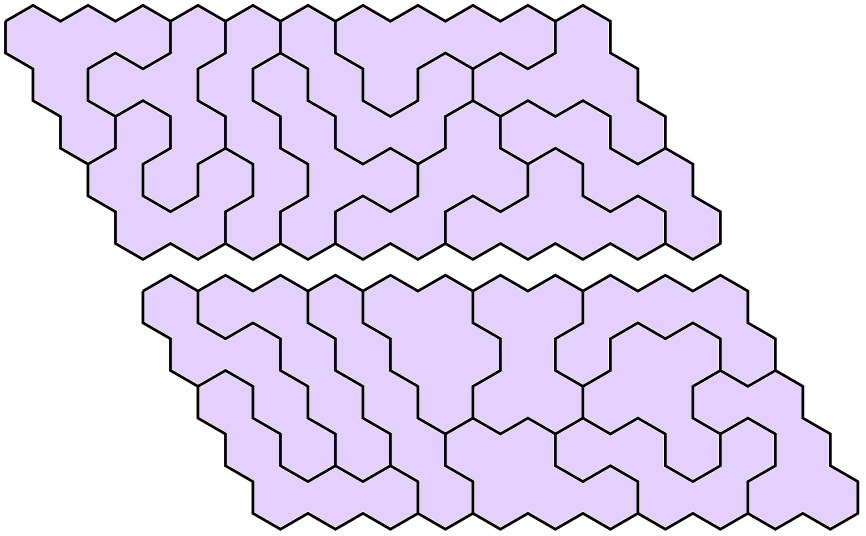
Things that aren't Parallelograms
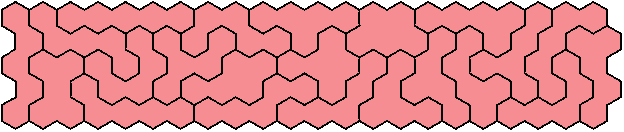
First off there's these approximations of rectangles. Here's the equivalent of the 5x22 and 11x10 to illustrate. The 10x11 and 22x5 (with the long edge being the more wiggly one) are no doubt possible but I haven't tried them.

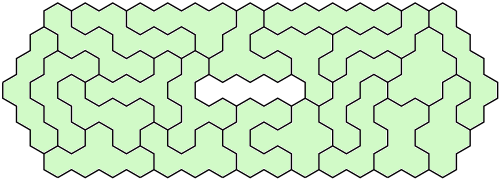
Then there's hexagons. This ones has an internal hole in order to bump the total area up - there may be 110-cell hexagons which work and have some symmetry, but I couldn't be bothered to search thoroughly for them.
Oh, and here's one more. A triangle-y type thing. With a hole that it's not possible to centre any better than I have here. Basically it was in my notebook (solved on 11/10/21 apparently) so I thought I'd digitise it and put it on here for completeness' sake.

Previous: Introduction to polyhexes | Next section: Hexahexes
[ Home > Polyhexes > Pentahexes ]
Lewis Patterson. Last updated 18/06/22.