Polyominoes 101 - The Absolute Basics

Contents
- Introduction
- Tetrominoes - The Starter Pack
- Pentominoes - The Original, Still the Best
- Hexominoes - The Big Leagues
- Heptominoes - The Even Bigger Leagues
- Octominoes - The Final Boss of Polyominoes?
- Beyond Octominoes...
Introduction
Yeah, an introduction to an introduction. What're you gonna do?
Polyominoes are the shapes made by joining squares edge to edge so their corners line up all nicely. I mean, you probably are already well aware of that fact judging by the fact you're on a site called 'polyominoes.co.uk'. But I'll give you the benefit of the doubt anyway. Just think Tetris, except you don't have to stop at four squares per piece. That's all polyominoes are. If you use equilateral triangles instead of squares you get a related set of shapes called the polyiamonds. Use hexagons, and you get the polyhexes. Easy peasy.
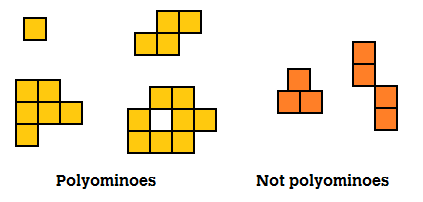
Polyominoes are named depending on how many squares they consist of. One square on its own is known as a monomino, two squares together makes a domino, three make a triomino (or tromino if you're weird), and so on and so on. There's a couple of quirks - the experts tend to use dekomino over decomino, and usage of enneomino vs. nonomino seems to be split roughly fifty-fifty. But other than that it's all standard prefixes. No sweat there.
Free, one-sided and fixed polyominoes
Cast your mind back to Tetris again. In the highly addictive world of Tetris, the 'S' and 'Z' shape are two very different pieces, as are the 'L' and 'J' shapes. But were these pieces to exist in the real world, as actual physical pieces, you could just flip one over to get the other. They'd be the same thing. So while the set of Tetris pieces consists of seven shapes - or tetrominoes, if we're being all fancy - a set of these pieces in the 3D world would have two duplicates, and only five distinct pieces. In the biz, we call the first set the one-sided tetrominoes and the second set the free tetrominoes. Because you're free to turn them over, I guess.
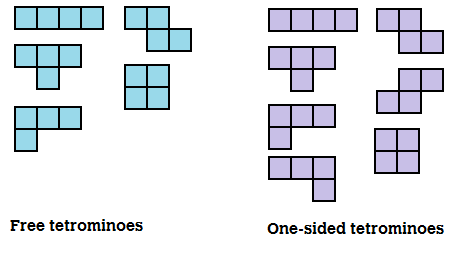
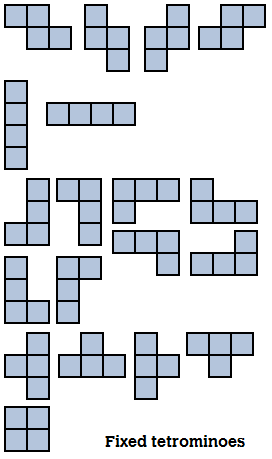
There's also a seldom talked-about third group of tetrominoes known as the fixed tetrominoes. These are the set you'd get if you counted rotations of the pieces as distinct, as well as reflections - i.e. the pieces are 'fixed' in space. Check these bad lads out:
Here are the numbers of polyominoes of each type, from the monomino all the way up to the dekominoes. As you can see, the numbers of each grow eye-wateringly quickly, especially in the case of fixed polyominoes.
| n-ominoes | Free | One-sided | Fixed |
|---|---|---|---|
| monomino | 1 | 1 | 1 |
| domino | 1 | 1 | 2 |
| triominoes | 2 | 2 | 6 |
| tetrominoes | 5 | 7 | 19 |
| pentominoes | 12 | 18 | 63 |
| hexominoes | 35 | 60 | 216 |
| heptominoes | 108 | 160 | 760 |
| octominoes | 369 | 704 | 2725 |
| enneominoes | 1285 | 2500 | 9910 |
| dekominoes | 4655 | 9189 | 36446 |
Links take you to various pages on this site focusing on these sets. Except the links in the bottom row that take you to the OEIS pages that have the counts for the free, one-sides and fixed n-ominoes for n > 10 in case you really need to know how many one-sided dodecominoes there are or something.
Tetrominoes - The Starter Pack
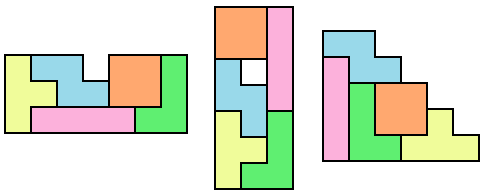
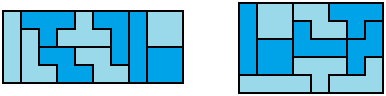
The five free tetrominoes will cover a total area of 20 square units, and these twenty square units can be arranged in all sorts of ways. There are some possibilities in the diagram below, including a 3x7 rectangle with a hole in it, a sort of staircase-looking thing and various other things.
In order to really get the most out of polyominoes, to really get balls deep into the art of solving, it is highly recommended that you get yourself a set of pieces of your very own to play with. I don't care what you make them out of - paper, cardboard, Lego, wooden blocks and glue - just make yourself some and see what you can do with them. You'll thank me later.
Parity: your new worst nightmare
So you've got your nice new shiny set of tetrominoes in front of you now. Hopefully you managed to knock a set together without injuring yourself with the scissors, or gluing too many fingers together in the process. And I bet you any money that one of the first things you tried with them was a nice tidy 4x5 rectangle, seeing as that would be twenty units and everything. And let's guess: you didn't manage.
Basically, there's this thing called parity which basically just exists to be the bane of any polyomino enthusiast's life. (And let's face it, if you've actually made a set you're well into enthusiast territory now. Your anorak is in the post.) In order to understand it just imagine placing each of your tetrominoes onto a chessboard. One that has squares the same size as the squares of the 'ominoes.
You'll notice that the square, the line, the S and the L shapes pieces will always cover two black squares and two white squares. No matter how you place them. Well, unless you do something wacky like put them down diagonally, but that doesn't count. But the 'T' tetromino will either cover three white squares and one black, or three black and one white. And it's this imbalance that causes all the headaches.
Imagine your precious 4x5 rectangle coloured with alternating colours like a chessboard - there will be ten white squares and ten black squares. Now place the T tetromino anywhere. This will leave uncovered seven of one colour and nine of the other. And the four remaining pieces are only going to ever cover equal amounts of black and white squares - eight and eight. So there's no way of getting all five tetrominoes into that 4x5 rectangle. Which is a bit of a turd in the punchbowl.
You get the same problem with the one-sided tetrominoes too, incidentally. And there's not really a lot you can do about it. Just got to be careful that the imbalance between numbers of black and white squares in your shape matches that of your piece set. Or you could do something rash and crazy, like introducing a second set of tetrominoes. This gives you a set of 10 pieces and an area of 40 units. And since you've got two 'T' tetrominoes to work with, you can use one to cover three white squares and the other to cover three black squares, and this leaves a balanced parity for the rest of the pieces to cover without a problem.
With this enhanced deluxe set a lot more shapes are possible. 4x10 rectangles, 5x8 rectangles, you can even do a 7x6 with a 1x2 central hole missing, a big old rectangular doughnut. But I'm not including an image of that. You'll have to find it yourself. And yeah, that's probably going to involve making a second set of tetrominoes (unless you've got a pencil and paper, an eraser and a whole lot of patience) but you're just going to have to get used to that. You can buy some polyform sets, but for others you'll just have to get your arts and crafts on.
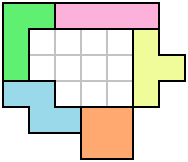
Of course, covering areas isn't the only thing you can do with polyominoes. With a single set of tetrominoes, an interesting challenge is to see how big an area you can surround. The image below shows a fenced-off area of 11 units, but that can probably be improved on.
(For this I used the additional criterion that the pieces must be connected edge to edge. If you instead opt to allow connections at diagonals then larger areas can be surrounded - my personal best is 15 but that too probably isn't optimal.)
Pentominoes - The Fan Favourites
The pentominoes are by far the most popular of the polyform sets, and it's not hard to see why. There are twelve of them (a really nice number of pieces for physical puzzles, not too few, not too many) and their total area is sixty units which divides up all sorts of nice ways. And there are no parity issues like in the case of the tetrominoes - odd-size polyominoes just don't seem to run into those as much. You can probably get a set of these made out of wood or plastic off the internet for fairly cheap if you don't feel like making them yourself, they're fairly ubiquitous like that. They often come in a nice little 6x10 tray which seems like a nice idea until you realise you have to solve the puzzle in order to put it away neatly. And these are, despite the relatively small number of pieces, fiendishly tricky little puzzles.
Rectangles
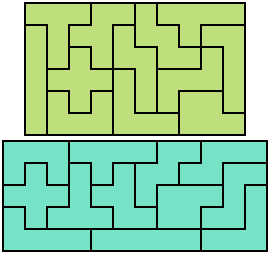
Four rectangles are possible with the pentominoes: 3x20, 4x15, 5x12 and 6x10. A 2x30 has the right area but several of the pentominoes are three cells long in both directions so they just wouldn't fit. And here we learn one of the rules of thumb when it comes to polyforms - thinner shapes generally have less solutions and are a little bit harder than short fat ones. In this case, the 6x10 has 2,339 solutions, the 5x12 has 1,010, the 4x15 has 368 solutions and the 3x20 has only two. The image below shows an example solution for the first two, but there are others to be found. And I've not put a solution for the 4x15 or 3x20 there, just to try and entice readers into solving them themselves (having said that, ten seconds of web searching could probably find you a solution if you were that way inclined.)
8x8 Chessboard Puzzles
A lot of early discussion about polyominoes happened in the pages of newsletters relating to chess-related puzzles, so it's little surprise that a lot of pentomino puzzles are based on the standard 8x8 chessboard. With its 64 squares, the area to be covered is just slightly more than the pentominoes alone can manage, but if you add in four monominoes (or one tetromino) to bring the total up, then you get a surprisingly versatile set of challenges.
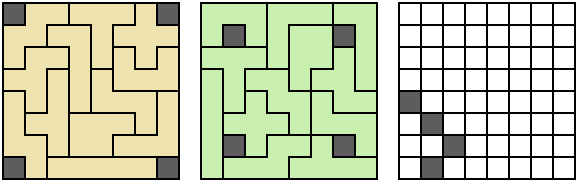
Firstly, just put four monominoes down wherever on the board. In most cases the resulting shape is tilable with the pentominoes, unless you've done something stupid like wall off an unreacheable space in the corner like in the image below.
Then, try dropping the square tetromino and fitting the pentominoes around it. This is always possible, no matter where you place the tetromino - in the middle, in a corner, even just randomly off-centre somewhere.
One thing those of you playing along at home may have realised is that finding solutions to pentomino puzzles can often feel a bit more like luck than skill. there are a few techniques if you can call them that - saving the p-shaped piece until near the end, pairing the C- and X-pentomino together - but it does admittedly often feel like pure chance when you stumble onto a solution. This randomness is remedied (somewhat) when you move on to sets of larger pieces...
Hexominoes - The Big Leagues
Once you've got the hang of pentominoes, and can knock together all manner of nice shapes without so much as breaking a sweat, then the obvious question begins to present itself. What's next? Maybe you've even augmented your set with the mirror-image pieces to make a full set of the 18 one-sided pentominoes, and solved a bunch of puzzles with them, the most difficult naturally being the task of playing with the set without succumbing to the urge to flip a piece over. By this point the seeds of polyomino addiction are unmistakably sown, and from here it's only a matter of time before you're carefully cutting the thirty-five hexominoes out from the back of a cardboard cereal box or something, salivating in anticipation of the wide world of new challenges these bigger, wigglier, more terrifying pieces will unlock. 210 units of total area... that's 2x3x5x7. It's practically perfect. Not in the mathematical sense of being the sum of its factors, but in the sense of being able to divide up so nicely. So many rectangles! So many activities! But lurking among these pieces lies something very sinister indeed, not immediately obvious to the untrained eye but coiled up and ready to reveal itself at the wost possible moment...
Parity 2: Electric Boogaloo
That's right. 24 of the hexominoes behave nicely, covering three white and three black squares when placed on the checkerboard from before. But the other eleven cover four of one and two of the other, and the fact that 11 is an odd number means that the total number of checkerboard squares of each colour the hexominoes cover is always unbalanced. Thus, we run into all sorts of problems.
However, so long as you're a bit careful about things, the hexominoes can still prove to be excitingly versatile. Just got to make sure that the numbers of white and black squares when you checkerboard-colour your construction differ by 2, 6, 10, etc.
Some shapes
Here's some sample shapes to get you started, all solvable with no parity issues or anything weird like that. I've just given the outlines, but if you click them there's a sample solution for each.
|
|
|
|
15 Puzzles
As 210 is (15x15)-15, it makes sense to try and solve configurations that are a 15x15 square with fifteen holes arranged artistically, a sort of bigger analogue to the pentomino chessboard problems mentioned earlier. See the image below for an example, and this page here for more possibilities.
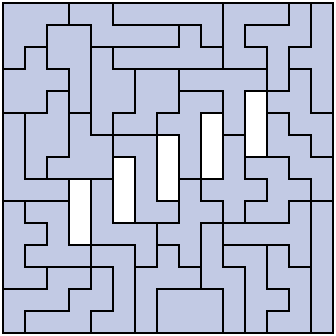
A little bit about solving technique
If you tried solving anything with the pentominoes you'll know that it sometimes seems more chance than skill when you eventually find a solution. However with the hexominoes (and larger sets of pieces!) there are some techniques that can be applied which reduce that sense of pure luck slightly. Emphasis on the 'slightly'.
Notice how in the above construction, nearly all of the pieces in the top left corner look like a 2x2 block with a few extra squares attached to them? These pieces, for whatever reason, just tile really nicely with each other. So by saving these pieces 'til the end so they're the last few you put in, you've essentially reduced a hard 35-piece puzzle into a rather more simple 7 or 8 piece puzzle. I mean, it's no guarantee it'll be any easier to solve, sometimes you can be left with the optimal pieces but the hole you've got left to fit them in just won't cooperate.
Actually, that's another thing. Keep an eye on the shape of the remaining space you have left. Don't leave deep inlets when you haven't got any long thin pieces to fill them. Don't let it get too wiggly an dconvoluted, especially near the end. The pieces you're saving for last will generally have pretty smooth flat sides so make sure the area you're leaving for them will be able to accomodate that. Solving in such a way that the last few pieces go in next to a completely flat edge of the puzzle can often be beneficial, if it's at all possible to do so.
And don't split the area into smaller areas or leave little 'islands' cut off from the remainder of the empty area - if the size of one those islands isn't a multiple of the size of a polyomino you've rendered the entire thing unsolvable.
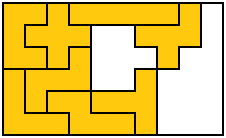
See that? That seven-cell hole is never going to get filled if all you can throw at it are 5-cell pentominoes.
A massively oversimplified example, but there you go.
Equally important is burning through the particularly horrible pieces early on - anything cross shaped or zig-zag shaped for example. As you play around and attempt to solve things you'll quickly get a feel for which pieces fall into this category. And it's worth making a point of using them as soon as you can - perhaps even starting with them if you can - because the longer you leave them the harder it will be to find a place for them later on.
See also: Combining the Pentominoes and Hexominoes into one big set
Heptominoes - The Even Bigger Leagues
This is the point where your instincts probably tell you to turn back. I mean, there's 108 of these wriggly monsters, and the hexominoes were already balancing nicely on that border between 'satisfyingly tricky' and 'agonisingly hard'. But then you think, 108 isn't that many. I mean, people do jigsaw puzzles with way more than 108 pieces without it being overwhelming. And while the hexominoes were hard, there were some nice little bits of technique that could be applied to solutions that the pentominoes didn't have - the whole piece ordering thing. And there'll be lots of heptominoes with flat, squarish parts that ought to make the endgame a little more tolerable... provided you get that far. And so you decide one day to bite the bullet and make (or buy, some places do them!) a set of heptominoes of your very own.
At this point it's useful to know that most major cities have places that do laser cutting, and that polyominoes are the number one easiest thing to draw into whichever CAD software. They all have that snap to grid option. And so, once you've finally got your clammy mitts around a set of heptominoes and you excitedly empty them out onto your living room table, you will notice something catching your eye. Something concerning. Not parity. But one particular piece.
This one, to be precise.

That kind of throws a spanner or ten into the works. I mean, we're not strangers to having the occasional hole in our constructions, but they were by choice, a purely sytlistic thing that we could opt into. It's different having the idea just thrust upon us like this whether we like it or not. But we've come this far now, we can't exactly just throw our arms up in the air and take up some other recreational mathsy type obsession (I hear speed-solving twisty puzzles is all the rage nowadays.) We're just going to have to roll with the hole.
Rolling with the Hole
Once we've calmed down, changed into some fresh pants and given it a bit of thought, the situation with the hole doesn't actually seem that bad. It's just a monomino-shaped hole. Just build it into the initial design, slap the harbour heptomino around it straight away, then we can solve the rest of the shape as normal.
Yeah, the harbour heptomino. It's one of the few heptominoes to have an official name. There's the straight heptomino which gets its name by virtue of a naming convention that starts with the straight triomino, then a few which got names because they do exciting things in Conway's Game of Life: The Pi heptomino, the bullet heptomino, the B-heptomino, the Herschel and maybe a few others too depending on who you ask. But individual polyominoes with widely-accepted names are something of a rarity.
There's polyominoes with unofficial nicknames, though... I reckon anyone who does any amount of manual solving on the regular comes up with their own little shorthand over time for identifying and describing pieces.
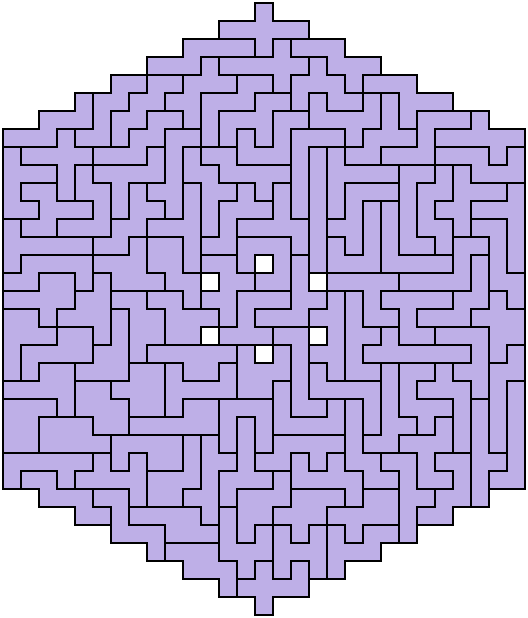
With a little flexibility in how many holes you permit in your constructions, the sky's the limit with these really. There's enough pieces and enough area that almost any shape can be approximated, so long as it isn't really really narrow or something. Here's a hexagon below (or a pixelated approximation of one), just to show that it's not all rectangles in the world of polyominoes.
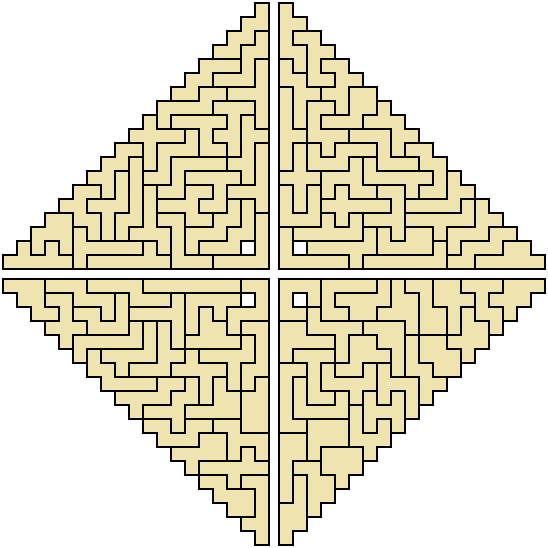
And here's four congruent triangles, all with one hole each. Configurations like this make for good challenging puzzles, several smaller identical shapes. In general, the more surface area, the larger pain in the neck it is to solve, but the greater satisfaction when you do eventually crack it.
If you really badly desperately want a hole-free heptomino construction, then you could always discard the harbour and solve using the remaining 107. Sadly, with 107 being prime, you're limited to only one rectangle - the 7x107. It's possible, it's a nice challenge, but unless you fancy getting real creative with other shapes it's all you're going to get. And if you're going to the effort of being creative you may as well do it with the full set of heptominoes.
Octominoes - The Final Boss?
By this point there aren't really any more huge surprises thrown your way as you add an extra square - octominoes are not that much different from heptominoes except there are a lot more of them. 369 to be precise, including six with holes. The first constructions done with the full set of octominoes were an assortment of shapes by David Bird in the '70s, and the 51x58 tiled by Michael Keller that graces the pages of the Kadon website, and that did a lot to spark my own interest in polyforms when I was little.
In terms of manual solving, the technique is fairly similar to the heptominoes, just way more time-consuming. Oh, and there's not really much scope for discarding the six holey octominoes and trying to make solid shapes with the remaining 363. This introduces (surprise, surprise) a parity issue. But by using the full set and just getting a little creative with the hole placement there's a lot of possibilities. One of which is below.
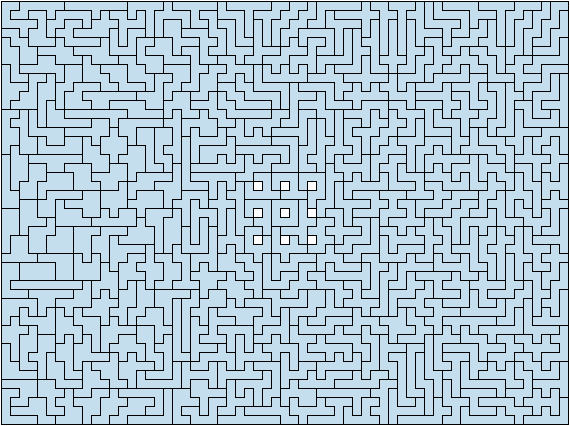
Beyond Octominoes...
With sets of pieces bigger than the octominoes you're sailing into comparatively uncharted waters. Well, not completely uncharted waters. Some brave souls have done jaw-dropping things with these sets - see this dekomino rectangle by Peter Esser, Polyominium' by Karl Wilk (more information part way down here), and even this physical set of dekominoes by Jean Carle, measuring 2 meters on a side! - but these are few and far between. The sheer number of enneominoes, even, is just a little bit beyond what most freely-available solvers are capable of handling, so even to find solutions via computer you'd have to put together your own program.
And when it comes to physical pieces, you're out of luck too. Kadon only do up to octominoes (or at least their site does, they may be able to whip up a bigger set if you asked them nicely) and making a set yourself on the cheap is either going to take a lot of cutting out or will give the peeps at your friendly neighbourhood laser cutting place a real headache. And even once you've contended with that uphill battle there's the logistics of solving a 1000+ piece polyomino puzzle. Say you need a specific piece, then you've got the joy of digging through an absolute heap of other very similar looking pieces for the exact one you want. This is bad enough even for octominoes - and the set I have is 3 colours so if you know the colour of the piece you want it alleviates the frustration somewhat. And of course then there's the final problem... finding a surface big enough to house your polyomino constructions.
The purely-computer-search people just might be onto something here...
[ Home > Polyominoes > Polyominoes 101 ]
Lewis Patterson. Last updated 04/02/23.